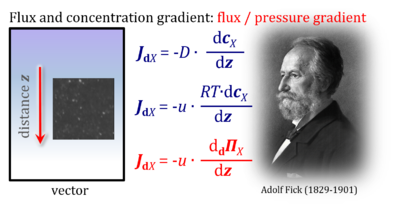Description
Pressure is a fundamental quantity expressing energy per volume. The SI unit of pressure is generally pascal [Pa] = [J·m-3]. The term 'stress' (mechanical stress) is used as a synonym for pressure (SI). Pressure is known in physics as mechanical pressure, which is force per area, p = F·A-1 [Pa] = [N·m-2]. In physical chemistry, gas pressure is defined as p = n·V-1·RT, where the concentration is c = n·V-1 [mol·m-3], R is the gas constant, and T is the absolute temperature, and RT is expressed in units of chemical force [J·mol-1]. van't Hoff's osmotic pressure assumes the same form applied to dissolved substances diffusing across a semipermeable membrane, but concentrations should be replaced by activities. The activity of dissolved gases is expressed by the partial pressure, where the solubility can be seen as an activity coefficient. Pressure appears explicitely or implicitely in all chapters of physics and physical chemistry. In contrast to the universal counterparts energy and force, however, the general connections between various isomorphic expressions of pressure remain poorly understood: Pressure is the concentration of the force at the point of action. More generally, pressure is the force times concentration at the interphase of interaction.
Abbreviation: p, P, Π [Pa]
Reference:
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. https://doi.org/10.26124/bec:2020-0002
- Gnaiger E (1989) Mitochondrial respiratory control: energetics, kinetics and efficiency. In: Energy transformations in cells and organisms. Wieser W, Gnaiger E (eds), Thieme, Stuttgart:6-17. - »Bioblast link«
Communicated by Erich Gnaiger (2018-09-16) last update 2022-10-26
SI units
- SI unit: Pa = J·m-3 = N·m-2 = kg·m-1·s-2
- 1 atm = 760 mmHg = 101.325 kPa
- {Quote} The pascal is also equivalent to the SI unit of energy density, the joule per cubic metre. This applies not only to the thermodynamics of pressurised gases, but also to the energy density of electric, magnetic, and gravitational fields. {end of Quote: https://en.wikipedia.org/wiki/Pascal_(unit) retrieved 2022-09-28}
Isomorphic laws and isomorphic formats
- In physical chemistry, gas pressure is defined by the fundamental Gas law, which can be expressed in different isomorphic formats, as: (1) p = C·kT (product of particle concentration [x·m-3] times kT [J·x-1]), and (2) p = c·RT (amount of substance concentration [mol·m-3] times RT [J·mol-1]). k and R are the Boltzmann constant and gas constant, respectively, and T is the absolute temperature.
- In addition to mechanical and gas pressure (hydrostatic pressure, barometric pressure, gas pressure), isomorphic pressures are distinguished as osmotic pressure, diffusion pressure, reaction pressure, and electric pressure.
- In ergodynamics, the pressure in a transformation, ΔtrΠX, is the product of free activity times force, ΔtrΠX = αX·ΔtrFX [mol·m-3 · J·mol-1 = J·m-3 = Pa] (Gnaiger 1989).
- Force and pressure are frequently confused. Isomorphic forces are expressed as exergy change per advancement, where advancement is expressed in transformation-specific motive units MU and a variety of different formats [J∙MU-1]. Free activity has the unit concentration of the transformation-specific motive unit [MU∙m-3]. Therefore, pressure as the product of isomorphic force and free activity has the unique unit pascal, [Pa] = [J∙m-3] = [J∙MU-1]∙[MU∙m-3]. Isomorphic forces are expressed in different units, such as mechanical [N]=[J∙m-1], electric [V]=[J∙C-1], particle [J∙x-1] or chemical [J∙mol-1]. In contrast, isomorphic pressures are universally expressed in the common unit pascal [Pa]. In this formal sense, isomorphic pressure is more fundamental compared to the concept of isomorphic force.
Force or pressure? - The linear flux-pressure law
- "For many decades the pressure-force confusion has blinded the most brilliant minds, reinforcing the expectation that Ohm’s linear flux-force law should apply to the hydrogen ion circuit and protonmotive force. .. Physicochemical principles explain the highly non-linear flux-force relation in the dependence of LEAK respiration on the pmF. The explanation is based on an extension of Fick’s law of diffusion and Einstein’s diffusion equation, representing protonmotive pressure ― isomorphic with mechanical pressure, hydrodynamic pressure, gas pressure, and osmotic pressure ― which collectively follow the generalized linear flux-pressure law."
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002
- » pressure = force × free activity
- The prevailing hypothesis of light at the time was that of Descartes. He believed that light was a 'pressure' transmitted through the transparent medium of the ether. Sight, he claimed, was due to this pressure impinging upon the optic nerve. - (White 1997: p 58-59)
- In both the "Hypothesis" of 1675 and the student notebook of 1661-65, Newton tended to attribute gravity to the pressure of a descending aetherial shower. - (Dobbs 1975: p 210)
- In the classical physicochemical literature, there is confusion between the terms force and pressure:
- "This force is called the pressure of the gas" by Maxwell (1867) - this is, indeed, correct, in contrast to the following pressure-force confusions:
- "This pressure is osmotic pressure. .. Osmotic forces are in fact .." by van't Hoff 1901.
- "pressures are attained which, too, are enormous under certain circumstances. Let us for example consider the process .. which, if electromotively active, would yield a galvanic cell with an e.m.f. of approximately .. 1.65 volts" by Nernst (1921).
- "Pressure-forces" by Einstein (1905).
- Presentation of Fick's law of diffusion (which represents a flux-pressure relationship) as a flux-force relationship by Prigogine (1967).
- Presentation of osmotic pressure as electrochemical potential difference by Mitchell (1966).
- Textbook aversion against the term 'osmotic pressure' illustrates the paradigmatic opposition against the concept of isomorphic pressure, and the suggested alternative term 'osmotic potential' leads directly to the prevailing pressure-force confusion - see Morris 1974 Edward Arnold.
- In the classical physicochemical literature, there is confusion between the terms force and pressure:
References
| Bioblast link | Reference | Year |
|---|---|---|
| Dobbs 1975 Cambridge Univ Press | Dobbs BJT (1975) The foundations of Newton's alchemy or "The hunting of the Greene Lyon". Reissued as a paperback 1983. Cambridge Univ Press Cambridge:300 pp. | 1975 |
| Einstein 1905 Ann Physik 549 | Einstein A (1905) Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann Physik 4, XVII:549-60. | 1905 |
| Fick 1855 Pogg Ann | Fick Adolf (1855) Über Diffusion. Pogg Ann 94:59-86. | 1855 |
| Gnaiger 1989 Energy Transformations | Gnaiger E (1989) Mitochondrial respiratory control: energetics, kinetics and efficiency. In: Energy transformations in cells and organisms. Wieser W, Gnaiger E (eds), Thieme, Stuttgart:6-17. | 1989 |
| Gnaiger 2017 MiP2017 | Gnaiger E (2017) Protonmotive force and chemiosmotic pressure: a generalization of non-ohmic flux control of the proton leak. MiP2017. | |
| Gnaiger 2020 BEC MitoPathways | Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002 | 2020 |
| Maxwell 1867 Phil Trans Royal Soc London | Maxwell JC ( 1867) On the dynamical theory of gases. Phil Trans Royal Soc London 157:49-88. | 1867 |
| Mitchell 2011 Biochim Biophys Acta | Mitchell P (1966) Chemiosmotic coupling in oxidative and photosynthetic phosphorylation. https://doi.org/10.1016/j.bbabio.2011.09.018 | 1966 |
| Nernst 1921 Nobel Lecture | Nernst W (1921) Studies in chemical thermodynamics. Nobel Lecture December 12, 1921:353-362. | 1921 |
| Prigogine 1967 Interscience | Prigogine I (1967) Introduction to thermodynamics of irreversible processes. Interscience, New York, 3rd ed:147pp. | 1967 |
| Van't Hoff 1901 Nobel Lecture | Van't Hoff JH (1901) Osmotic pressure and chemical equilibrium. Nobel Lecture December 13, 1901:5-10. | 1901 |
| White 1997 Fourth Estate | White M (1997) Isaak Newton. The last sorcerer. Fourth Estate, London 402 pp. | 1997 |
- Bioblast links: Concentration and pressure - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Concentration
- » Volume
- » Activity
- » Concentration
- » Density
- » Mole
- » Molar mass
- Concentration
- Pressure
- Solubility = concentration/pressure
- General
- » Boltzmann constant
- » Energy
- » Force
- » Gas constant
- » Work
- General
- Related keyword lists
MitoPedia concepts:
MiP concept,
Ergodynamics