Description
A number N is a count NX [x] divided by the elementary entity UX [x]. X must represent the same entity in both occurences. The elementary unit [x] cancels in the division by simplification, such that numbers (for example, numbers 8 or 24) are abstracted from the counted entity X. The concept of number is tightly entangled with units, counts and entities.
Abbreviation: N
Communicated by Gnaiger Erich (2020-06-30) last update 2024-04-24 in: Anastrophe XX Entity X and the elementary unit x of X-mass Carol
Canon III: In a nutshell — NUCE
Is 6 a number? Are 6 and 8 numbers?
- It is difficult to separate the concept of 'number' from the realization of numerals: number-words and number symbols. There are two sides of each number: (1) In the physical realization, a number is expressed in code, with different names (words) in different languages, and different numerals (made of one or more digits) in different numeral systems (types of notation). If 6 and 8 are numerals, then 6 and 8 are the physical realization of the concept number 6 and number 8. (2) In the mental realization, a number is a concept independent of the form in which it is expressed. N is the symbol for number, representing the set of all nondimensional numerical values without units.
- Six stones, Ns = 6 x, is a count of stones, with the result that there is a number of 6 elementary entities Us identified as stones, which is a count of 6 stones. Since this count yields a "number of 6 stones", the "stones" are the countable entities with the single individual stone as the Euclidean unit Us, and 6 is the corresponding number, expressed by the numeral 6 with the meaning 'a numerical value of 6'. I need help for clarification, if there is any difference between a specific number and its numerical value.
- 8 is a numeral in the Arabic numeral system. The number symbols are called numerals; a numeral is the figure of a number, with different notation types used as a figure (VIII and 8 for Roman and Arabic numerals; 八 and 捌 for practical and financial Chinese). Consider the symbol 9 written into MitoPedia as elementary entity X=9. Then counting "9 9 9 9 9 9 9 9" (unary numeral system) yields a count N9 = 8 x, and the count N9 [x] divided by the elementary entity U9 [x] yields the number N = 8, using the figure eight as the numeral in Arabic notation type. To illustrate further, the symbol (or character) 8 is used as (1) the numeral 'eight' as before; (2) one of two symbols in the numeral 80 or 'eighty' in the decimal numeral system; a symbol used eight times in the numeral 88888888 with the meaning 'eight' in the unary numeral system. The human number concept has not only quantitative cardinal meaning related to the count (8 or 24 elementary entities), but is applied in expressing the ordinal rank of objects or events arranged in a sequence (the 24th day of a month; in the Fibonacci-sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, .. the 8th number is 13, whereas in an older representation of the Fibonacci-sequence 1, 1, 2, 3, 5, 8, 13, 21, .. the 7th number is 13, the 5th number is 5), and in nominal labelling (drawing lot #24; serial number #8.007; DOI number doi10.26124bec2020-0001). Numbers for counting (1, 2, 3, 4, 5, 6, 7, 8, ..) are unified multiplicities required for cardinal counting or ordinal nomination of the endpoint in a sequence. It is debatable, if one can have a zero count; a no-object, or an object that is not there to be counted. If this possibility is not denied, then counting numbers are equivalent to natural or whole numbers (0, 1, 2, 3, 4, 5, 6, 7, 8, ..). Numbers are represented by numerals as words, iconic symbols, or entirely abstract symbols. The word 'snake', the numeral 'eight', the symbol '8' written in ink on a piece of white paper are as different from the real "object snake", as they differ from the "concept ////////", or "concept §§§§§§§§", or "concept 88888888", or "concept ∞∞∞∞∞∞∞∞" (unary numeral system), or "concept 'number eight'". We are so deeply used to these symbols, that we easily take the iconic or abstract symbol 8 — that represents the number eight — as the number eight itself, without a need to give the symbol 8 an interpretation and ask for its meaning. The numeral 8 has to be distinguished from it's interpretation as the number that the numeral represents.
Formats and meanings of numbers
- It is instructive to compare some terms related to count and number, to units and first numbers in sequence in different languages, illustrating the depth of interpreration and meaning residing in the treasury of words (Wortschatz) and etymology. Many words in English are rooted in Latin, compared to German which includes more terms with roots in the Northern languages (Table 1). If you are multilingual, try this with other languages. Observe how predominant are the roots count and Zahl, unit and eins. These terms are highly differentiated. What makes this even more surprising or dubious, is why the formalized language of the International System of Units (SI) lacks a concept, symbol, and proper unit for the quantity 'elementary entity' UX.
- Number words (words denoting specific numerals) are simple in English and German up to a dozen (one to twelve, eins bis zwölf) and are compound above (thirteen, dreizehn).
- Table 1. Count, unit, number, and number one: knowledge and meaning within words of different languages
Term English German Comment count NX count (account) Anzahl (Konto) generating a count counting (paying) zählen (zahlen) narrating a count telling, recounting erzählen Telling a tale and Zahl have a common Proto-Indo-European root (tala-zahla). unary numeral system unary numeral system unäres, monadisches Zahlensystem Numeral system using a single symbol. unit unit Einheit Single undivided whole; a member of a group; a unit quantity as a standard of measure. unity unity, uniqueness, oneness Einheit, Einigkeit, Einzigartigkeit Being or appearing as one (Latin unus, one). union union Vereinigung Being one; international union .., IUPAC (Latin unus, one). unified united vereinigt Assembled in one (Latin unus, one). unitary unitary einheitlich number N number Zahl antonym: letter / Buchstabe numeral X numeral, cipher, digit, notation, form, entity-type Ziffer (Arabic sifr, from India for zero; 〇), chiffre interpreting a numeral decipher entziffern, dechiffrieren (from French) number series one, 1; two, 2; three, 3 eins, 1; zwei, 2; drei, 3 (Proto-Indo-European origin) ordinal numbers first (primary), 1st; second (secondary), 2nd; third, 3rd; fourth, 4th erste, zweite, dritte, vierte One / eins is not used for the 'first' / 'erste' (antonym last / letzte); two is not used for the 'second' / but zwei is used for 'zweite'; further up, three / drei is used for "third" / "dritte"; etc. The words third upwards are not only ordinal numbers but are also used for fractions. the feeling of being alone loneliness Einsamkeit antonym: Gemeinsamkeit single single, separate einzeln, einzig, einfach antonym: double /doppelt (Latin singulus, one, consisting of one unit) singular singular Einzahl antonym: plural / Mehrzahl (Latin singulus, one, consisting of one unit) single component detail Einzelheit uniqueness singularity, uniqueness Einmaligkeit 1 x, 2 x, 3 x once, twice, three times einmal, zweimal, dreimal
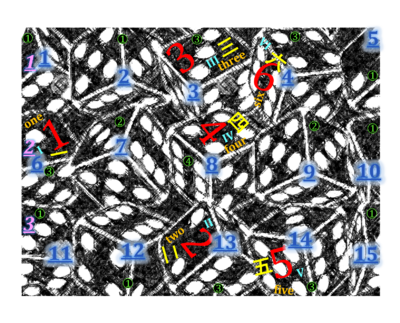
- Figure 1. Formats and meanings of numbers.
- Counting and notation types: (1.1) dice, (1.2) Roman numerals, (1.3) Mandarin-Chinese signs, (1.4) Arabic numerals, (1.5) English number-words. The dice format requires hardly any interpretation, since the signal for counting is given in a series of linear expansion; this works well up to :::, but does not work for 66 or 666. Similarly, Roman and Mandarin symbols from I to III do not need interpretation due to the signal for counting, but IV to VI is more complex in Roman and Mandarin notations by compression required for extension towards higher numbers. Interpretation of Arabic numerals and English words needs learning from beginning with 1 and one, since the formal relation to counting is abandoned in favor of reduction; these investments pay off in the long run — once Arabic numerals have been learned, these symbols can be recognized and distinguished most rapidly, be written most economically, and be extended to high numbers by combination in the decimal number system. English words are much less economical in writing, but they connect isomorphically the image of the written number-word with the acoustic form of the spoken number-word.
- Cardinal counting and ordinal ranking of dice: There are 15 dice in the figure. Dice 1 to 5 are in row 1; dice 6 to 10 are in row 2; dice 11 to 15 are in row 3.
- Nominal labelling: Dice of tye (1) are with single notation and positioned on the margin of the figure; (2) dice with single notation and positioned in the center of the figure; (3) dice with multiple notations and positioned on the margin of the figure; (4) dice with multiple notations and positioned in the center of the figure.
- Number magnitude and space: Dice with different notation types have a numerical magnitude that increases with their position in space from left to right. This spatial association is less pronounced for Mandarin notation type.
- Sex of numbers and numerical parity: Even numbers such as 6 are associated with female sex, and are likened more than odd numbers such as 3, which connotate masculinity (Wilkie 2015 Front Psychol). Even odd and even numbers are gendered. Isn't it odd to be the odd man?
- Dice have figures 1 to 6 on their six sides (Figure 1). These figures can be expanded backwards (downwards?) from 6 to 1 to 0. One way to get a zero with a die is to (1) push it off the table. Other ways are to (2) scrape off any dot on any side of the die, (3) cover any dot on any side of the die with an untransparent square, (4) put the untransparent square on the table and ignore the die (Table 2, 1st row).
- Emptiness and zero are a non-matter of Zen, and that's where the concept of the number 〇 comes from. We cannot count a dot that is not there. Therefore, zero cannot be a count. In addition, zero does not count: NX + 0 x = NX. But zero devours a count in multiplication: NX · 0 = 0 x. And zero undetermines a count in division: NX / 0 x = ∞. Division by zero — the smallest — provides the 'definition' of infinitiy — the largest of all infinities.
- The presentation given above in practical form needs further consideration in canonical form.
- "Zero cannot be a count" has to be generalized: A number is not a count. A number cannot be added to a count, as much as a number cannot be added to a mass, or a mass cannot be added to a volume. If two things are to be added, the two occurrences have to be expressed in the same quantity and units. Addition requires an identity of quantity and units. Back to the X-mass party: mX + 4 is as meaningless as mX + 0. Zero is neither a mass nor a count, it is a number. A mass of 4 kg of peares can be added to a defined mass of apples, both occurrences expressed in an identical unit [kg]. But neither 4 nor 0 can be added to a defined mass of apples, or to a defined number of apples. The numbers 4 and 0 are unitless. The mass of X is expressed in the SI unit [kg]. The "number of X" is a count expressed in the canonical unit [x]. A number of 4 apples, Na = 4 x, can be added to a number of 5 pears, Np = 5 x; then the total number of pieces (= the total count) of fruit in the Assembly A is NA = 4 x + 5 x = 9 x. N is a number (4), NA is a count (4 x). Thus NX + 0 is as meaningless as NX + 4.
- Can a count have a value of NX = 0 x? — This is an entirely different question. To be answered, it is a CASE like any case with numbers. And in any case, extending the perspective helps to answer this particular question.
- First extension — from statics to dynamics: Consider an open System H with exchange of X=B across the system boundaries. Let the volume VB of a sample of elementary entities B be negligible compared to the total volume of H and keep H at constant volume, temperature, and pressure. When H receives a tiny volume ΔVB of B, this is something positive for the volume of B in H. When the system H looses B, this is negative for H. If we consider the nature of entity-type B to be rigid, such that the volume VUB is constant during the external transfer of B between H and the environment, then we have simplified the external transfer process under consideration: the volume VUB is very small, but it is fixed, and the volume VUB cannot ever have a negative sign in this non-imaginary scenario. While the volume VUB is fixed, the volume-balance of B in H is zero, if nothing happens. Then the change of volume of all entities B in the system is ΔVB = 0 L. When some external pressure on B pushes B into system H, then the volume of B inside H increases, such that the change of the volume of all B entities in H is larger than zero, ΔVB > 0 L. Having loaded system H with entities B, the tide may change, the sign of the external pressure is reversed, and the Budget B becomes negative with a negative volume change of B in the system, ΔVB < 0 L. The change in volume ΔVB of B in the system can be positive, zero, or negative; but neither the volume of B in H can ever be negative, nor can the volume per elementary entity B ever be negative. Summary: a change in volume as defined can be negative, zero, or positive.
- Second extension — from volume to count: accepting all simplifications in the scenario described above, there is a fixed relationship between the volume VB of B in H and the count NB of B in H. For the first CASE term Counting, ΔVB and ΔNB can have positive or negative values. For the second CASE term Assembling, we are looking at an ensemble of an open system in its environment. For the third CASE term Sampling, it is essential to separate a sample of B in a defined experimental system. The fourth CASE term is the Entity, and definition of the elementary entity of X is a fundamental prerequisite for the counting of objects or events. The sampling may or may not be directly connected with counting: It is possible to count the number of elementary entities added into or removed from the experimental system. A count cannot be negative, but the change of the count in H can have a negative value.
- ΔNB is zero x in a static system.
- Can NB be equal to zero x? Let your bank account be H and NB the number of Bank-Euros on your account. If your NB drops to zero depends on many things. Zero x is a Bad possibility, but still Better than a negative account of B. For the fourth CASE term Entity, is takes experience to disentangle NUCE — in a nutshell: disentangling Numbers, Units, Counts, and Entities is at the core of CASE.
- The presentation given above in practical form needs further consideration in canonical form.
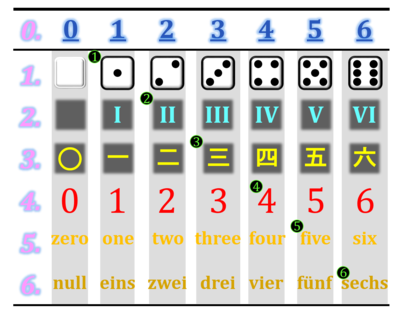
- Table 2. Symbols for numbers — numerals — notations.
- The header of the table shows underlined numerals indicating the ordinal rank of each column. The index column on the left shows italic numerals as nominal labels as an index for the format of each row. Each column within the table represents a number in different notations. Counting all symbols within the table yields a cardinal number of 42 number-symbols, or 56 number-symbols when the header and index column are included. Each number is represented by "::: VI 六 6 six sechs" symbols, which illustrates that a symbol cannot be a number. "::: VI 六 6 six sechs" can be seen as a single though complex numerical symbol (it is composed of six symbol-components) representing the number 6, or as six different symbols, each representing the number 6 in a different format:
- Symbols for 1 to 6 on dice showing figures of dots (pips) as cardinal numerals for counting. The numeral 0 does not exist on a numerical system of dice, it is a no-dot or even a no-die, since no die has seven sides. The dots yield iconic symbols or figures as counting-numerals, such that the count of dots yields the explicit code for interpretation of each symbol. It is suggestive to deduce, that dice deliver an intuitive understanding of the numbers 1 to 6, but this is wrong, since the dots on dice yield the experience of counts from 1 dot to 6 dots. How do we get from a number of dots to a number?
- Roman numerals have the same problem with the number 0 as a die. Lines are shown for counting-numerals as iconic symbols I, II, and III, comparable to the dots on a die. IV shows a line as a negative integer on the left of V. This is part of the code to decipher Roman numerals, but the code is more complex. It is generally thought, that seven symbols are used in the Roman numeral system: I (1), V (5), X (10), L (50), C (100), D (500), M (1000). However, X can be seen as two times V (V + Λ), in which case the Roman numeral system uses only six different symbols.
- The Chinese Mandarin includes zero as a number 〇, and shows counting-numerals as lines comparable to the Roman iconic counting-numerals I, II, and III. Higher numbers are represented as abstract symbols comparable to Arabic numerals, or as symbols that may be seen as words.
- The Arabic number system adopted the zero from Asian Indian mathematicians. Cipher (German Ziffer) is rooted in the Arabic sifr, which stems from India for zero. The Arabic numeral 1 can be seen as an iconic symbol or counting-numeral comparable to the Roman I and Chinese —.
- English words.
- German words.
- Nominal numbers 1 to 6 in circels label six categories of cells in the table:
- (0) The symbol for number 0 is outside of this system and does not count.
- (1) The symbol for number • that is labelled with nominal number (1) in rank 1 and the 1. line.
- (2) The symbol for number II that is labelled with nominal number (2) in rank 2 and the 2. line.
- (3) The symbol for number 三 that is labelled with nominal number (3) in rank 3 and the 3. line.
- (4) The symbol for number 4 that is labelled with nominal number (4) in rank 4 and the 4. line.
- (5) The symbol for number five that is labelled with nominal number (5) in rank 5 and the 5. line.
- (6) The symbol for number sechs that is labelled with nominal number (6) in rank 6 and the 6. line.
- Binary notation is not considered, since it does not fit into Table 2. The word 'one' is represented as 01101111 01101110 01100101 in binary code, whereas the numeral 1 is 00110001. Do you see any 'number 1' in binary code?
- A fundamental problem in the concept of 'number sense' is in NUCE, a confusion of numbers, units, count, and entity. In any CASE, the concept of 'number sense' should be replaced by a 'sense' that operates on the level of assembling entities into units for counting - the number is the last thing that makes sense, even if it comes first in NUCE: Number—Unit—Count—Entity.
Does a number make sense?
- Numbers cannot be seen, heard, touched, tasted, or smelled; they do not emit or reflect signals; they leave no traces. So what kind of things are they? These are the central philosophical questions about numbers. Plausible combinations of answers have proved elusive. Marcus Giaquinto, in Kadosh 2015 Oxford Univ Press
- Something heavy makes sense. We feel the weight on the basis of interpreting sensory signals. Mass does not make sense. Even if we are familiar with the concept of mass, we tend to say 'weight' for some kg of potatoes, and tend to forget what we learned about weight as a force in contrast to the base quantity mass. Even if we tend to forget similarly what we learned about irrational or imaginary numbers, "numerousness, like shape, size and color, is a basic property of our perceptual world" (Agrillo 2020 PLOS ONE). Numerousness is so basic, that we perhaps never had to learn to think deeply about the sense of numbers — not in the sense of numerology, but in the sense of a sensory and neuronal processing system for numerosity. The predecessors of numerical cognition in animals and human infants rely on finite and iconic representations that are limited to cardinality and do not support a unified concept of number. Extraction of numerical information from optical images and acoustic frequencies may not depend initially on actual counting, but represents the pillars in the evolutionary framework of counting. Thus numbers are like counts in the looking glass or events in the echo. It makes sense to think that the object or event is the cause for the mirror image or echo. But if the mirror image looks at me, how do I resist identifying me with the image? If a number reflects a count, how do I avoid confusion between count and number? If a looking glass may cause confusion, then numbers and counts are entangled on multiple angels. The SI gives the count a unit of a number: The unit of a count is devoured by the number one, the number reflects the count, the entity is number one - the looking glass is substituted by the magic NUCE-kaleidoscope.
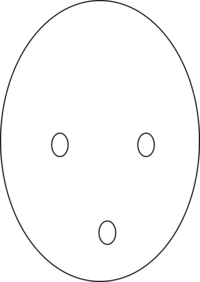
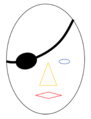
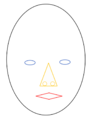
- We learn early about odd and even numbers: Numerical parity becomes an integral part of number representation from about the 4th grade onward (Wilkie 2015 Front Psychol). But structural encoding of faces occurs between 4 and 6 months of age (Farzin 2012 J Vision). A first step is to discern an odd and even number of objects nested in a single face. Visual object categorization and semantic identification require Counting-Assembling-Sampling of Entities (CASE). In Figure 4 there are four objects (Counting). But CASE makes us seeing immediately two eyes as a single pair (Counting and Assembling) and identify one mouth and the pair of eyes as components of a face or person for Sampling an Assembly rather than considering a single eye, very close to an automatic reflex involved in defining an elementary entity (Figure 5). CASE makes us look into a single unit 'face', without ambiguitiy of seeing two eyes as two faces (Figure 6). This would be different, if our species is born and lives with a single eye patch mask (Figure 7). Assembling in CASE of two nose holes occurs in parallel with the pair of eyes (Figure 8), and a deeper level of assembling, when the nose is recognized not only as a pair of holes but as an assembled object (Figure 9). As in Figure 9, the nose with two nose holes is recognized — when it comes to couning noses — as a single elementary entity rather than seeing three objects within the face (Figure 5). For fast recognition, it is sufficient to grasp a sort of nose holes in a type of nose in a kind of face. Counting, assembling and sampling (sorting) ears and eye brows and hair get more complex with differentiation of types, and with taking a face as a CASE of a kind of person (Figure 10).
Figure 5. H(1M,1A[2E]): Unit face as the Highest-level System H. The four objects are not seen as 4 (1 vertical oval + 1 mouth + 1 eye + 1 eye), but are a CASE: accounted for as 1M + 1A(2E) (Counting and Assembling: 2 eyes = 1 Assembled pair of eyes), and associated with a single face {Stacking: H(1M,1A[2E])}. A new face is sorted further as part of a new H=person: H(1F[1M,1A{2E}]). The Counting-Assembling-Stacking Experience (CASE) goes on.
Figure 6. Two faces: one eye — one face. The three objects seen in the face are not interpreted as 1 + 2. Based on CASE, the part of the face seen is recognized as a single Highest-level System H with two objects, Mouth and Nose, and one assembly A(2E) that is completed by the invisible second eye — H(1M,1N,1A[2E]).
- Figure eight makes sense, polishing the gold cathode of a polarographic oxygen sensor (POS) not in the sense of 8 times, but by moving along figure eight lines.
A taxonomy of numbers
- Number theory knows many families of numbers, not restricted to integers, primes, binaries, and further conventional taxa (Table 3). There are excessive numbers (the sum of its divisors is greater than the number itself; for 12: 1+2+3+4+6 = 16), defective numbers (the sum of its divisors is less than the number itself; for 10: 1+2+5 = 8), slightly defective numbers (the sum of its divisors is only one less than the number itself; for 4: 1+2 = 3), and perfect numbers (the sum of its divisors is exactly the number itself, which is rare; for 6: 1+2+3 = 6; for 28: 1+2+4+7+14 = 28). It is not known why slightly excessive numbers do not exist. Closely related to the perfect numbers of Pythagoras are Fermat's friendly or amicable numbers (220 and 284, which are "pairs of numbers such that each number is the sum of the divisors of the other number" (Singh 1997). 26 is the only sandwiched number between a square number (52 = 25) and a cube number (33 = 27). There are sociable numbers (three or more numbers that form a friendly closed loop). There are excessive prime numbers (4n+1) and defective prime numbers (4n-1). All non-primes are composite numbers, since they are multiples of numbers. Gottlob Frege is considered to be the inventor of the definite definition of a number in terms of sets.
- Table 3. Undebatable kinds of numbers
Class Example Comment number for counting, natural number 1, 2, 3, 4, .. Positive integers. All natural numbers are whole numbers. whole number 0, 1, 2, 3, 4, .. Natural numbers including zero. All whole numbers are integers. negative integer -1, -2, -3, -4, .. Negative integers are integers excluding whole numbers. integer .., -4, -3, -2, -1, 0, 1, 2, 3, 4, .. Negative integers and whole numbers. Orders: (1) even numbers, (2) odd numbers, (3) prime numbers. All integers are rational numbers. rational number -2/1, -0.5, 0.0, 0.3, 1/2, 7.8 Any number that can be written as a ratio of two integers — where the denominator must not be zero —, or as the resulting fraction written with decimal digits after the decimal dot. All rational numbers are real numbers, and are not imaginary numbers. irrational number square root of 2; √2 Irrational numbers cannot be written as a ratio of two integers; the have an infinite number of decimal places. real number Real numbers include all types of numbers listed above and are defined as points on a line from -∞ to +∞. immaginary number square root of -1 An imaginary number squared yields a negative real number. complex number Complex numbers are combinations of real and imaginary numbers. They live on the number plane (Singh 1997).
The energy of numbers
- Energy is a fundamental quantity of physics with the SI unit joule [J]. The first law of thermodynamics makes the familiar statement that energy is constant, in the sense that it cannot be produced or destroyed, as long as one stays away from the domain of relativity theory. The second law of thermodynamics, however, claims that a particular form of energy (better termed exergy) can be and must be destroyed as long as the final state of equilibrium is not reached. Thus the term 'energy' leads to lots of confusion, since there are different forms of energy (Figure 11).
- It is tempting to consider numbers with different energies in analogy to the different forms of energy. This may resolve the difficulty to distinguish a number from its numerical value. Counting nuts or counting stones, and the numerals on regular dice as symbols for the numbers 1 to 6 provide a help to get a feeling for the energy of numbers. Numbers with different energies are in different states of realization. To avoid confusion between a pure number n and a count NX, consider the definition of a count as the product of a number n and an elementary entity UX. The symbol n for pure number may be replaced by the symbol N, if confusion with amount of substance nX is to be avoided.
Physical numbers
- The potential energy of a stone mounted at a paricular height is the energy that can be retrieved potentially when coupling its fall to the ground with an energy-transforming process, without which the energy is dissipated as heat. Consider the potential number as any of the six numbers on a die, which may show on the top after throughing the die. The potential number is the single number of the set of possible numbers, which will be realized after throughing the die. The set of possible numbers on a physical device limits the range of potential numbers that can possibly be realized. This kind of potential number belongs to the order of physical numbers. Another physical number is the static number, which is the numerical value on top of a die realized after having thrown the die, or the numerical value of a count of stones in a box. A static number has a defined numerical value, whereas a potential number has only the probability that a particular numerical value will be realized. But if the die is not thrown, the value of n is not known, if the stones in the black box are not counted, the count NX has no defined value.
- A dynamic number or dynamic numerical value may be seen as the number added to the side of a die when making the die. This is the highly dynamic process of creating a new number. The number of numbers (this is a count) in the universe is not a constant. Type a digital number into your computer — push a button and you are the creator of a new number. You may cut a number into stone or write a number on paper — you are a number maker. If you burn a regular wooden die, there will be a loss of six numbers in the world. Less dramatically, a dynamic number is related to events. When a stone is moved into or out of a box, then this is an event that may help to count the change of the number of stones in the box. From the perspective of the box, throwing a stone into the box is a count with a positive number, picking a stone out of the box is a count with a negative number. Any number of, is not a number, but is a count; the count has a numerical value which is a number of something physically real.
Virtual numbers
- Virtual numbers are abstract and used by mathematicians. More specifically, an abstract number is a virtual number of a virtual die realized without throwing the die, or a virtual number of abstract stones in an abstract box. All types of physical numbers can be imagined or realized as virtual numbers. Mathematical numbers, however, are virtual numbers realized without any abstraction from a physical thing as a theoretical reference. Since the universe contains a limited number of particles, an infinite number can only be a mathematical number used by mathematicians, and not an abstract number with a physical reference of the imagination in the real world.
The Zen of Zero
- Table II.0. There is no symbol for zero. 〇 is one.

- Table II.1. There is a number of 〇
Figure 13. Nested numbers or: There was 1 beer, there is 0 beer.
References
| Bioblast link | Reference | Year |
|---|---|---|
| Agrillo 2020 PLOS ONE | Agrillo Christian, Piffer Laura, Bisazza Angelo, Butterworth Brian (2020) Evidence for two numerical systems that are similar in humans and guppies. PLOS ONE 7:e31923. | 2020 |
| Baroody 1983 J Research in Mathematics Education | Baroody AJ, Price J (1983) The development of number–word sequence in the counting of three-year-olds. J Research in Mathematics Education 14:361-8. | 1983 |
| Bell 1999 Springer | Bell John L (1999) The art of the intelligible. An elementary survey of mathematics in its conceptual development. Springer Science+Business Media Dordrecht:249 pp. | 1999 |
| Brown 2018 Metrologia | Brown RJC (2018) The evolution of chemical metrology: distinguishing between amount of substance and counting quantities, now and in the future. Metrologia 55:L25. https://doi.org/10.1088/1681-7575/aaace8 | 2018 |
| Brown 2021 Metrologia | Brown RJC (2021) A metrological approach to quantities that are counted and the unit one. Metrologia 58:035014. https://doi.org/10.1088/1681-7575/abf7a4 | 2021 |
| Bureau International des Poids et Mesures 2019 The International System of Units (SI) | Bureau International des Poids et Mesures (2019) The International System of Units (SI). 9th edition:117-216. ISBN 978-92-822-2272-0 | 2019 |
| Cooper 2012 Synthese | Cooper G, Humphry SM (2012) The ontological distinction between units and entities. Synthese 187:393–401. https://doi.org/10.1007/s11229-010-9832-1 | 2012 |
| Farzin 2012 J Vision | Farzin Faraz, Hou Chuan, Norcia Anthony M (2012) Piecing it together: Infants' neural responses to face and object structure. J Vision 12.6. | 2012 |
| Giaquinto 2015 Oxford Univ Press | Giaquinto M (2015) Philosophy of number. In Kadosh RC, Dowker A (ed) The Oxford handbook of numerical cognition. Oxford Univ Press:17-32. https://doi.org/10.1093/oxfordhb/9780199642342.013.039 | 2015 |
| Gnaiger 2020 BEC MitoPathways | Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002 | 2020 |
| Gnaiger 2020 MitoFit x | Gnaiger E (2021) The elementary unit — canonical reviewer's comments on: Bureau International des Poids et Mesures (2019) The International System of Units (SI) 9th ed. https://doi.org/10.26124/mitofit:200004.v2 | 2021 |
| Gong 2019 J Numerical Cognition | Gong Tianwei, Li Baichen, Teng Limei, Zhou Zijun, Gao Xuefei, Jiang Ting (2019) The association between number magnitude and space is dependent on notation: evidence from an adaptive perceptual orientation task. J Numerical Cognition 5:38–54. | 2019 |
| Grosholz 2007 Oxford Univ Press | Grosholz Emily R (2007) Representation and productive ambiguity in mathematics and the sciences. Oxford Univ Press 312 pp. | 2007 |
| Kadosh 2015 Oxford Univ Press | Kadosh Roi Cohen, Dowker Ann, ed (2015) The Oxford handbook of numerical cognition. Oxford Univ Press:1185 pp. | 2015 |
| Singh 1997 Fourth Estate | Singh Simon (1997) Fermat's last theorem. Fourth Estate, London 340 pp. | 1997 |
| Spiegelhalter 2015 Profile Books | Spiegelhalter David (2015) Sex by numbers: What statistics can tell us about sexual behaviour. Profile Books, London 368 pp. | 2015 |
| Wilkie 2015 Front Psychol | Wilkie James EB, Bodenhausen Galen V (2015) The numerology of gender: gendered perceptions of even and odd numbers. Front Psychol 6:810. | 2015 |
MitoPedia concepts:
Ergodynamics