Description
An elementary entity is an entity of type X, distinguished as a single unit of countable objects (X = molecules, cells, organisms, particles, parties, items) or events (X = beats, collisions, emissions, decays, celestial cycles, instances, occurrences, parties). "An elementary entity may be an atom, a molecule, an ion, an electron, any other particle or specified group of particles" (Bureau International des Poids et Mesures 2019). An elementary entity, therefore, needs to be distinguished from non-countable entities and the general class of entities X. This distinction is emphasized by the term 'elementary' (synonymous with 'elementary entity') with symbol UX and elementary unit [x].
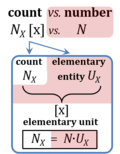
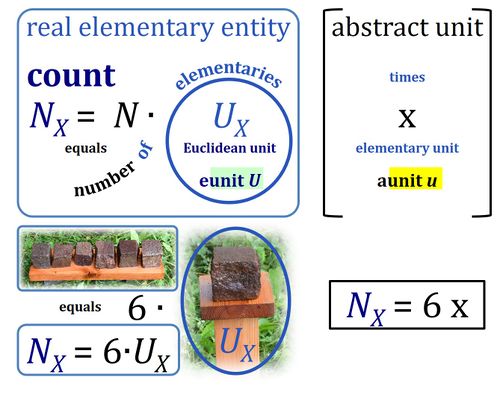
If an object is defined as an assembly of particles (a party of two, a molecule as the assembly of a stoichiometric number of atoms), then the elementary is the assembly but not the assembled particle. A number of defined elementaries UX is a count, NX = N·UX [x], where N is a number, and as such N is dimensionless, and N is a number (stop) and is not 'a number of ..'. Elementaries are added as items to a count. The elementary UX has the dimension U of the count NX. The elementary UX has the same unit [x] as the count NX, or more accurately it gives the count the defining 'counting-unit', which is the 'elementary unit' [x]. From the definition of count as the number (N) of elementaries (U) of entity type X, it follows that count divided by elementary is a pure number, N = NX·UX-1. The unit x of a count can neither be the entity X nor a number. The elementary of type X defines the identity X of the elementary UX with the unit 'elementary unit' with symbol [x]. Since a count NX is the number of elementary entities, the elementary UX is not a count (UX is not identical with N·UX).
Abbreviation: UX [x]
Reference: BEC2020.1 doi10.26124bec2020-0001.v1, Gnaiger MitoFit Preprints 2020.4
Communicated by Gnaiger Erich (2020-07-10) last update 2020-08-11 in: Anastrophe XX Entity X and elementary unit x of X-mass Carol
Entity-type, elementary entity, and elementary unit
- In Euclid's Elements (Book VII) a "unit" is defined as 'a single individual thing'. Take 'individual thing' as equal to elementary entity or simply elementary. The Euclidean unit is tightly conjugated with the individual thing. In diametrical contrast, the SI unit is completely abstracted from any individual elementary entity. The SI unit is entirely disjugated from any individual type of thing. Put one SI unit into an experimental system to obtain a volume of one unit [m3] or run an experiment with a mass of one unit [kg], it may be a unit of anything. 1 kg is always 1 kg of any entity-type X. X does not even have to be known to measure mass in units of kg. For the unit volume in units of meters cubed or dm3 (liter), the independence of the unit from entity X is pushed to the limit: a system with the size of a unit volume may contain no single individual thing, not anything at all — a liter of nothing or a liter of something is invariably a liter. Neither the unit of volume (liter) nor the unit of mass (kg) are units of a single individual thing.
- As cognitional tools and not as acutally proposed terms, you can think of the Euclidean unit as the real "eunit" of countable things, in contrast to the abstract "aunit" expressing a corresponding quantity of anything.
- An attempt to unite these opposite meanings of the term 'unit' appears like an alchemical Mysterium Coniunctionis (Jung 1963). How can the conjunction of the opposites — the unit of a single individual thing and the unit of anything — be realized? As Carl Gustav Jung has pointed out, a guiding principle of the early constructive alchemists was the combination of the practical and theoretical in the process of experiments and personal experience. To realize something means to achieve a conjunction of experimental physical realization (making it real, based on a perceptual definition of things in an experimental system) and theoretical psychological realization (becoming aware of the real, based on a conceptual definition of terms in a theoretical system). This understanding provides the key to the conjunction of Euclid's and SI's concepts of units.
- Quote SI p. 124: "To be of any practical use, these units not only have to be defined, but they also have to be realized physically for dissemination. In the case of an artefact, the definition and the realization are equivalent – a path that was pursued by advanced ancient civilizations. Although this is simple and clear, artefacts involve the risk of loss, damage or change. The other types of unit definitions are increasingly abstract or idealized. Here, the realizations are separated conceptually from the definitions so that the units can, as a matter of principle, be realized independently at any place and at any time. In addition, new and superior realizations may be introduced as science and technologies develop, without the need to redefine the unit. These advantages – most obviously seen with the history of the definition of the metre from artefacts through an atomic reference transition to the fixed numerical value of the speed of light – led to the decision to define all units by using defining constants." Quote SI p. 124: "The use of a constant to define a unit disconnects definition from realization."
- Quote SI p. 202: "Experimental methods used for the realization of units and which use equations of physics are known as primary methods. .. Traditionally, a unit for a given quantity was taken to be a particular example of that quantity, which was chosen to provide numerical values of common measurements of a convenient size. Before the rise of modern science, units were necessarily defined in terms of material artefacts, notably the metre and kilogram for length and mass, or the property of a particular object, namely the rotation of the earth for the second. Even at the origin of the metric system at the end of the 18th century it was recognized that a more desirable definition of a unit of length for example would be one based on a universal property of nature such as the length of a pendulum beating seconds. Such a definition would be independent of time and place and would in principle accessible all over the world. At the time, practical considerations resulted in the simpler, artefact definitions for the metre and the kilogram and the second remained linked to the rotation of the Earth. It was only in 1960 that the first non-material definition was adopted, namely the wavelength of a specified optical radiation for the metre" (Bureau International des Poids et Mesures 2019).
- The abstract SI unit is tightly linked to the Euclidean unit by the physical realization. It is a mind-boggling thought, that "the definition and the realization are equivalent" in the case of an artefact, and that any errors inherent in artefacts have been removed from the SI base units by conceptual separation of the definition and realization of the unit, completed in the SI definitions of 2019-05-20.
- We see Euclid's unit in reflections with the SI's unit not merely in a looking glass, but in a kaleidoscopic interplay of Number, Unit, Count, Entity — NUCE (in nuce), which remains a CASE to this day (CASE represents the Counting-Assembling-Sampling Experience).
- The elementary entity UX is distinguished from entity-type X. Dual-message code may lead to misunderstanding depending on context. For example, take O2 as entity X. VO2 and mO2 are the volume [m3] and mass [kg], respectively, of a sample of pure O2. For the volume, it is important to specify the gaseous state at a given temperature and pressure, whereas these specifications are irrelvant for the quantity mass. For volume and mass it needs to be ensured that there is a pure sample of oxygen (X = oxygen), but the specification of the elementary entity is irrelevant. The values of oxygen volume and oxygen mass remain independent of having in mind molecules of O2, atoms of O, or charges of oxygen. Observe now the subtle transition from extensive quantities Qu (VO2 and mO2) to elementary quantities QX (NO2 and nO2).
- NO2 is the count of O2 molecules. NO2 is equal to the number of elementary entities UO2. The elementary UO2 for the count of oxygen molecules is different from the elementary UO for the count of oxygen atoms. UO2 and NO2 are expressed in the unit 'elementary unit' [x]. nO2 is the amount of O2 expressed in the unit mole [mol]. nO2 is equal to NA-1 times the number of elementary entities UO2.
- X = ce in 'cell mass' is normally understood as meaning "the mass of all entities of entity-type ce in a sample", mce [kg]. In contrast, X = body in the context of body mass and body mass index (BMI) is used in dual-message code, mbody. Body mass with dual-message code means the mass of all entities of entity-type human body, mbody [kg], divided by the number of bodies, NBody, which leads to the explicit canonical expression MUBody = mbody·NBody-1.
- Colour code: Colour red may be used in X, indicating that the term entity or symbol X are used in dual-message code, meaning both entity-type and elementary entity. When specifying "single item X" it is sufficiently clear that X is used in dual-message mode, and the term "number of X" is equally clear to meaning "number of elementaries of type X", NX = N·UX-1. Similarly, in the term "O2 flow per cell" IO2/ce" it is sufficiently clear that ce is used in dual-message code.
Base quantities and count
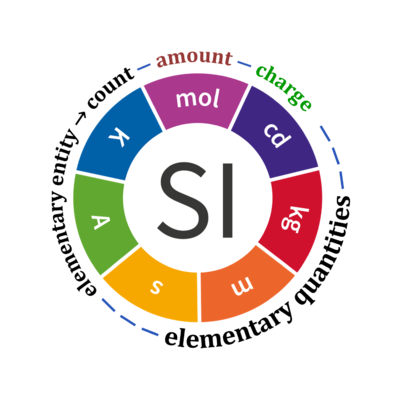
Quantity Symbol for quantity Q Symbol for dimension Name of abstract unit uQ Symbol for unit uQ [*] elementary entity *,$ UX U elementary unit x count *,$ NX = N·UX X elementary unit x amount of substance *,§ nX = NX·NA-1 N mole mol charge *,€ Qel = zX·e·NX I·T coulomb C = A·s length l L meter m mass m M kilogram kg time t T second s electric current I I ampere A thermodynamic temperature T Θ kelvin K luminous intensity Iv J candela cd
- [*] SI units, except for the canonical 'elementary unit' [x]. The following footnotes are canonical comments, related to iconic symbols.
- * For the elementary quantities NX, nX, and Qel, the entity-type X of the elementary entity UX has to be specified in the text and indicated by a subscript: nO2; Nce; Qel.
- $ Count NX equals the number of elementary entities UX. In the SI, the quantity 'count' is explicitly considered as an exception: "Each of the seven base quantities used in the SI is regarded as having its own dimension. .. All other quantities, with the exception of counts, are derived quantities" (Bureau International des Poids et Mesures 2019 The International System of Units (SI)). An elementary entity UX is a material unit, it is not a count (UX is not a number of UX). NX has the dimension X of a count and UX has the dimension U of an elementary entity; both quantities have the same abstract unit, the 'elementary unit' [x].
- § Amount nX is an elementary quantity, converting the elementary unit [x] into the SI base unit mole [mol] using the Avogadro constant NA.
- € Charge is a derived SI quantity. Charge is an elementary quantity, converting the elementary unit [x] into coulombs [C] using the elementary charge e, or converting moles [mol] into coulombs [C] using the Faraday constant F. zX is the charge number per elementary entity UX, which is a constant for any defined elementary entity UX. Qel = zX·F·nX
References
| Bioblast link | Reference | Year |
|---|---|---|
| Brown 2018 Metrologia | Brown RJC (2018) The evolution of chemical metrology: distinguishing between amount of substance and counting quantities, now and in the future. Metrologia 55:L25. https://doi.org/10.1088/1681-7575/aaace8 | 2018 |
| Brown 2021 Metrologia | Brown RJC (2021) A metrological approach to quantities that are counted and the unit one. Metrologia 58:035014. https://doi.org/10.1088/1681-7575/abf7a4 | 2021 |
| Cooper 2012 Synthese | Cooper G, Humphry SM (2012) The ontological distinction between units and entities. Synthese 187:393–401. https://doi.org/10.1007/s11229-010-9832-1 | 2012 |
| Gnaiger 2020 BEC MitoPathways | Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2. https://doi.org/10.26124/bec:2020-0002 | 2020 |
| Gnaiger 2020 MitoFit x | Gnaiger E (2021) The elementary unit — canonical reviewer's comments on: Bureau International des Poids et Mesures (2019) The International System of Units (SI) 9th ed. https://doi.org/10.26124/mitofit:200004.v2 | 2021 |
| BEC 2020.1 doi10.26124bec2020-0001.v1 | Gnaiger E et al ― MitoEAGLE Task Group (2020) Mitochondrial physiology. Bioenerg Commun 2020.1. https://doi.org/10.26124/bec:2020-0001.v1 | 2020 |
- Jung CG (1963) Mysterium Coniunctionis: an inquiry into the separation and synthesis of psychic opposites in alchemy, 2nd ed. Collected works of CG Jung, London: Routledge. ISBN 978-0-415-09115-2
- Bioblast links: SI base units - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Entity, count, and number, and SI base quantities / SI base units
Quantity name Symbol Unit name Symbol Comment elementary UX elementary unit [x] UX, UB; [x] not in SI count NX elementary unit [x] NX, NB; [x] not in SI number N - dimensionless = NX·UX-1 amount of substance nB mole [mol] nX, nB electric current I ampere [A] A = C·s-1 time t second [s] length l meter [m] SI: metre mass m kilogram [kg] thermodynamic temperature T kelvin [K] luminous intensity IV candela [cd]
- Fundamental relationships
- » Avogadro constant NA
- » Boltzmann constant k
- » elementary charge e
- » Faraday constant F
- » gas constant R
- » electrochemical constant f
- Fundamental relationships
- SI and related concepts
MitoPedia concepts:
Ergodynamics